今回の記事では、線形代数学で扱う行列式の基礎について解説します。
行列式は、行列に関するさまざまな問題を解く際に必要となるもので、特に逆行列や固有値の計算、連立方程式の解の存在条件などに関わっています。
本記事では、行列式の基本的な定義から計算方法などを、初学者向けにわかりやすく解説していきます。
行列式を知らない方や計算方法を知りたい方はぜひご覧ください!!
この記事を書いている人
・京都大学理系学部
・大学で線形代数学を学習中
行列式とは
基本的な定義
行列式(ディターミナント)とは、正方行列に対して定義されるスカラー値(数値)のことです。
決して、方程式やベクトルのことではありません。
また、行列がどのような性質を持っているかを一つの数値で表す指標と考えることができます。
そして、行列式は、次のようにさまざまな場面で役立ちます。
・逆行列の存在確認: 行列式がゼロでない場合、その行列は逆行列を持ちます。逆に、行列式がゼロである場合、その行列は逆行列を持ちません。
・線形独立性の判定: 行列式を使うことで、ベクトルが線形独立かどうかを判定できます。
・行列による変換の影響: 行列式の符号や値から、行列による空間変換の性質(反転するか、縮小・拡大するか)を判断できます。
これらは、行列式の応用編として記事にしますので今回は取り扱いません。
行列式の表記
行列\(A\)の行列式は、\(|A|\) や \(det(A)\) と表記します。
この記事では、今後\(det(A)\) と表記します。
行列式の簡単な計算方法
行列式を計算する方法を説明していきます。
今回の記事では、2次、3次正則行列と対角行列の行列式の計算のみを扱います。
というのも、4次以上の正則行列の行列式の計算は簡単ですが、煩雑なので今後別の記事に書きます。
2次正則行列の行列式
まずは最も基本的な2×2行列の行列式の計算方法から説明します。2×2行列は次のように表されます。
\[
A = \begin{pmatrix}
a & b \\
c & d
\end{pmatrix}
\]
この行列 \( A \) の行列式は、次の式で計算されます。
\(det(A)\) = \(ad – bc\)
具体例として、次の行列 \( A \) を考えてみます。
\[
A = \begin{pmatrix}
3 & 8 \\
4 & 6
\end{pmatrix}
\]
この行列の行列式は次のように計算されます。
\(det(A)\) = \(3 × 6\) – \(8 × 4\) = \(18 – 32\) = \(-14\)
このように、2×2行列の行列式は簡単に計算できます。
つまり、次のようにたすき掛けで計算できるということです。
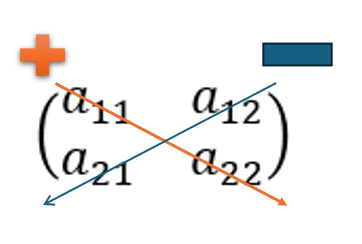
3次正則行列の行列式
次に、3×3行列の行列式の計算方法を見てみましょう。3×3行列は次のように表されます。
\[
B = \begin{pmatrix}
e & f & g \\
h & i & j \\
k & l & m
\end{pmatrix}
\]
3×3行列の行列式は、次のような公式で計算します。
\(det(B)\)
= \(e × (i × m – j ×l) – f \times (h × m – j × k) + g × (h × l – i × k)\)
=\(eim + hlg + kjf – gik – fhm – elj\)
この公式をサラスの公式といい、有名な公式です。
これもたすき掛けで次の図のようになります。
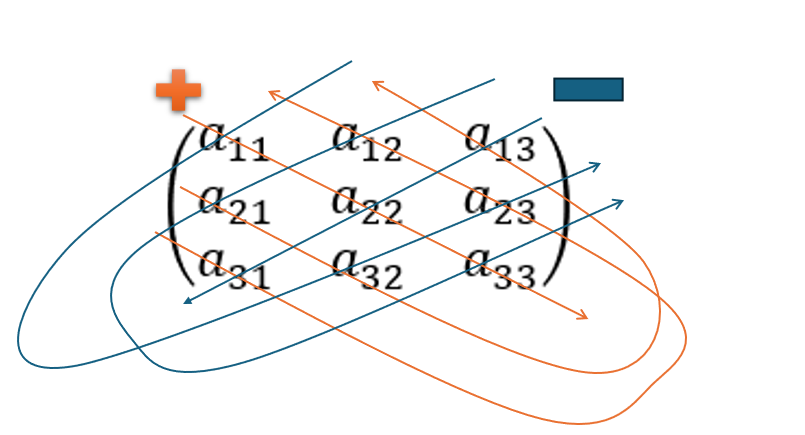
※図の汚さはご了承ください。
では、具体的に計算していきましょう。
具体例として、次の行列 \( B \) を考えてみます。
\[
B = \begin{pmatrix}
2 & 1 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end{pmatrix}
\]
この行列の行列式は次のように計算されます。
\(det(B)\)
= \((2 × 5 × 9 + 4 × 8 × 3 + 7 × 6 × 1 ) – (3 × 5 × 7 + 1 × 4 × 9 + 2 × 8 × 6)\)
=\((90 + 96 + 42 ) – (105 + 36 + 96)\)
=\(-9\)
このように、3×3行列の行列式は煩雑ではあるものの、たすき掛けで計算できます。
対角行列の行列式
次は、対角行列の行列式について解説します。
ここで、対角行列とは、対角成分以外のすべての要素がゼロである行列を指します。
例えば、次の3×3の対角行列 \( D \) を考えます。
\[
D = \begin{pmatrix}
d_{11} & 0 & 0 \\
0 & d_{22} & 0 \\
0 & 0 & d_{33}
\end{pmatrix}
\]
対角行列の行列式は、対角成分の積で求められます。つまり、行列 \( D \) の行列式 \( det(D)\) は次のようになります。
\(det(D)\) = \( d_{11} × d_{22} × d_{33} \)
具体例として、次の対角行列 \( D \) を考えてみましょう。
\[
D = \begin{pmatrix}
2 & 0 & 0 \\
0 & 5 & 0 \\
0 & 0 & 7
\end{pmatrix}
\]
この行列 \( D \) の行列式は次のように計算できます。
\(det(D) = 2 × 5 × 7 = 70 \)
このように、対角行列はシンプルに対角成分を掛けるだけで計算できます。
まとめ
今回は、行列の基本的な定義や表記方法から簡単な行列式の計算を解説しました。
今後、行列式の詳しい性質やより煩雑な行列式の計算を解説していきます。



コメント