このページでは写像の概念と単射・全射・全単射の定義を図を用いて初学者向けにわかりやすく解説しています。
理系の大学生なら線形代数学や微分積分の授業の始めに習う範囲でしょう。写像の概念を理解できれば今後の勉強も順調に進むので頑張ってください!
写像とは
写像とは集合から集合への対応関係を表す数学的な概念です。高校までは写像を関数と呼んでいたでしょう。
例えば、集合 A から集合 B への写像を fとして、fは集合 Aの各要素を集合 Bの要素に1対1で対応させます。これを数式で表すと、次のようになります。
$$
f: A \rightarrow B
$$
ここで、集合 Aを定義域、集合 B を値域と呼びます。これは中学でも習いますね。
具体的な例を見てみましょう。例えば、A = {1, 2, 3} と B = {a, b, c} という集合があり、写像 f が次のように定義されているとします。
$$
f(1) = a, \quad f(2) = b, \quad f(3) = c
$$
この場合、A の各要素が B の要素に対応しているのが分かるでしょうか。
簡単なイメージ図はこのようになります。
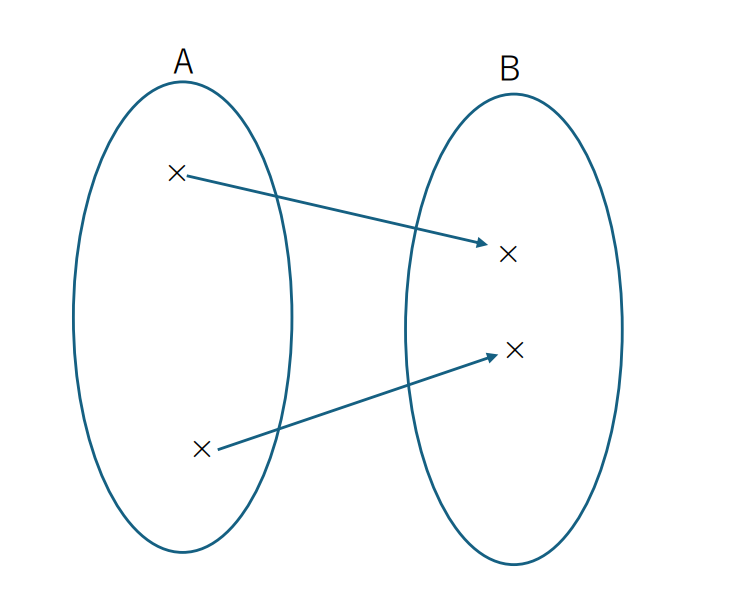
集合から集合への対応を表してますね。
次からは写像の種類について解説していきます。
単射
単射とは異なる A の要素が異なる B の要素に対応する写像である。
これを数式で表すと次のようになります。
$$
\text{任意の} \ a_1, a_2 \in A \ \text{に対して} \ f(a_1) = f(a_2) \Rightarrow a_1 = a_2
$$
対偶を取ると
$$
a_1, a_2 \in A\ \text{に対して} \ a_1 \neq a_2 \Rightarrow f(a_1) \neq f(a_2)
$$
これらは定義であり、少しわかりにくいと思った方は下のイメージ図を見てください。
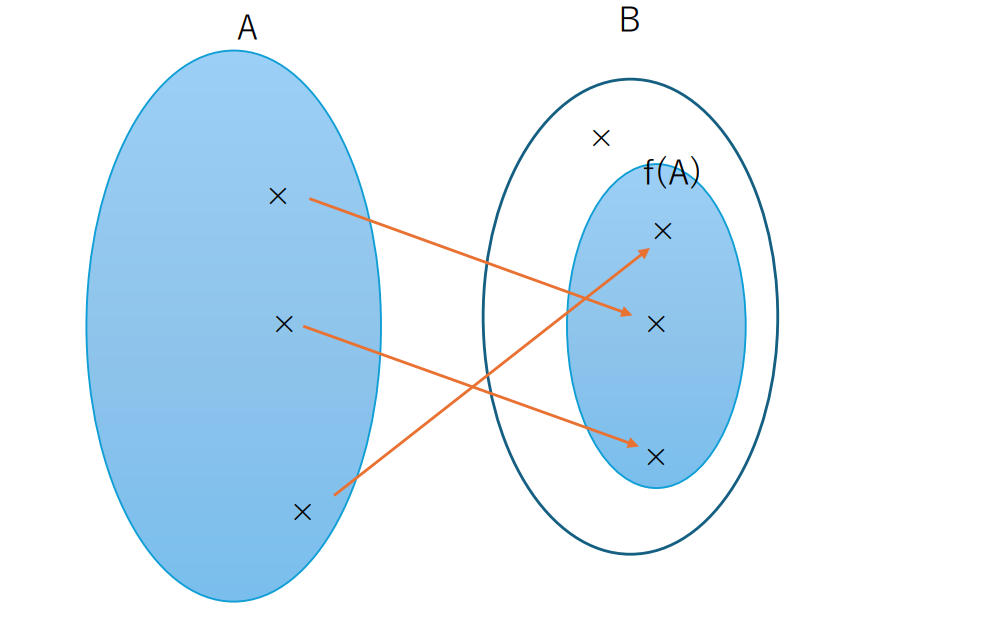
Aの異なる要素がf (A) (⊂B)の異なる要素に対応しているのが分かるでしょう。これが単射です。
単射の例をあげると、A = {1, 2, 3} と B = {a, b, c, d} のとき、写像 f が次のように定義されているとすると、写像fは単射です。
$$
f(1) = a, \quad f(2) = b, \quad f(3) = c
$$
これで分かったでしょうか。
全射
次は全射について解説します。
全射とは、値域のすべての要素が少なくとも1つの定義域の要素に対応している写像です。
数式で表すと次のようになります。
$$
\text{任意の} \ b \in B \ \text{に対して} \ \text{ある}\ a \in A \text{で} \ f(a) = b \text{が存在する}
$$
再びイメージ図で表すと次のようになります。
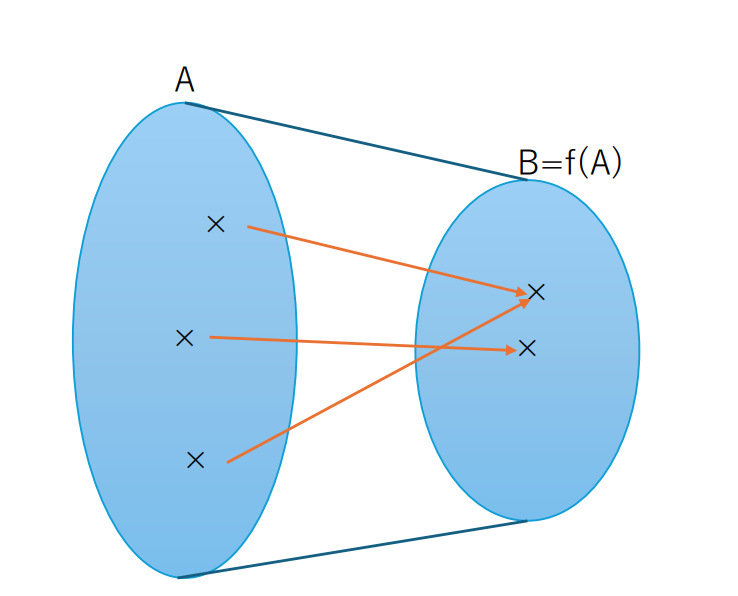
図のように値域B (=f (A))の1つの要素に定義域Aの複数の要素が対応することがあるのが、全射なのです。
つまり、値域のどの要素にも対応する要素がAの中に必ず存在するのです。
全射の例をあげると、A = {1, 2, 3} と B = {a, b} のとき、写像 f が次のように定義されていると、写像fは全射となります。
$$
f(1) = a, \quad f(2) = b, \quad f(3) = a
$$
全単射
次は3つの写像のうち最後の全単射について解説していきます。
全単射とは単射かつ全射のことです。つまり、集合Aと集合Bの要素が1対1対応していることです
では、イメージ図を見てみましょう。
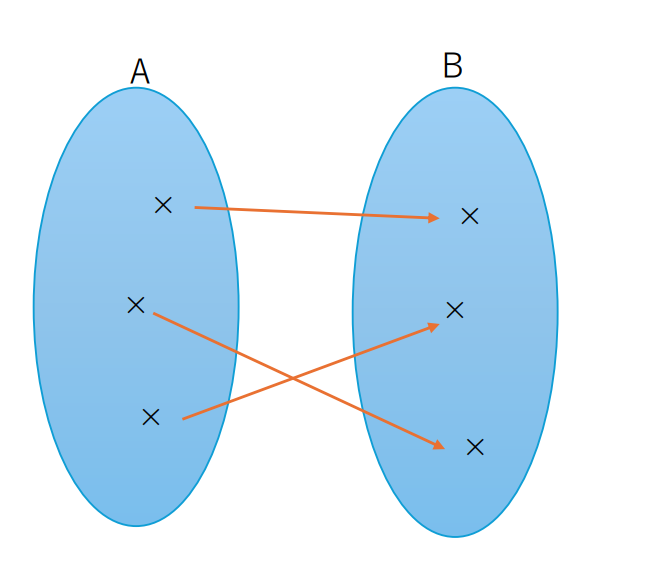
イメージ図のように集合Aのすべての要素が集合Bの異なる要素に対応しているので単射であり、集合Bのすべての要素が集合Aに対応しているので全射でもあることが分かりますよね。
逆写像
最後に、おまけで逆写像について解説します。
逆写像とは文字通り、元の写像の対応を逆にした写像のことです
例えば、写像 f が次のように定義されているとすると、
$$
f: \{1, 2, 3\} \rightarrow \{a, b, c\}
$$
$$
f(1) = a, \quad f(2) = b, \quad f(3) = c
$$
この場合、逆写像 は次のようになります
$$
f^{-1}(a) = 1, \quad f^{-1}(b) = 2, \quad f^{-1}(c) = 3
$$
このように逆写像は
$$
f^{-1}: B \rightarrow A
$$
と表せます。
写像fの逆写像が常に存在するわけではないことに注意が必要です。
写像fの逆写像は写像fが全単射の場合でしか存在しません。また、fの逆写像も全単射です。
したがって、写像fが全単射ならば、
$$
\text{任意の} a \in A, \text{任意の} b \in B \text{で} \ f(a) = b \iff f^{-1}(b) = a
$$
が成立します。
まとめ
今回は今後の数学の勉強の土台となる写像と写像の種類について解説しました。
今回分かるようになったこと
・写像の概念
・単射、全射、全単射の概念、イメージの理解
・逆写像について



コメント