今回は線形代数の基本的な概念である線形写像や核について、具体例をふまえながら初学者やある程度授業で習ったことのある人向けに解説します。
練習問題も作ったのでぜひ挑戦してください。
写像とは何なのかまだ理解できていない人は、先に下の記事を読んでくださいね。
この記事を書いた人
・京大現役合格
・大学で数学・物理化学を学習中
線形写像と像、核
線形写像と像
線形写像と像についてそれぞれ定義を説明します。理解が難しいのでイメージ図ものせておきました。
線形写像の定義
線形写像f は、あるベクトル空間 Vから別のベクトル空間 W への写像で、次の2つの性質を持ちます。
1. 加法性: 任意のベクトル \( \mathbf{u} \) と \( \mathbf{v} \) に対して、
\[
f(\mathbf{u} + \mathbf{v}) = f(\mathbf{u}) + f(\mathbf{v})
\]
2. スカラー倍: 任意のスカラー \( c \) とベクトル \( \mathbf{v} \) に対して、
\[
f(c \mathbf{v}) = c f(\mathbf{v})
\]
上の条件2つとも成立するとき、写像fは線形写像であるといえます。
像の定義
像(イメージ)とは、線形写像 f によって得られる全てのベクトルの集合です。
\[
\text{Im}(f) = \{ \mathbf{w} \in W \mid \mathbf{w} = f(\mathbf{v}) \text{ 、 } \mathbf{v} \in V \}
\]
定義ではわかりにくい方は下のイメージ図を見てください。
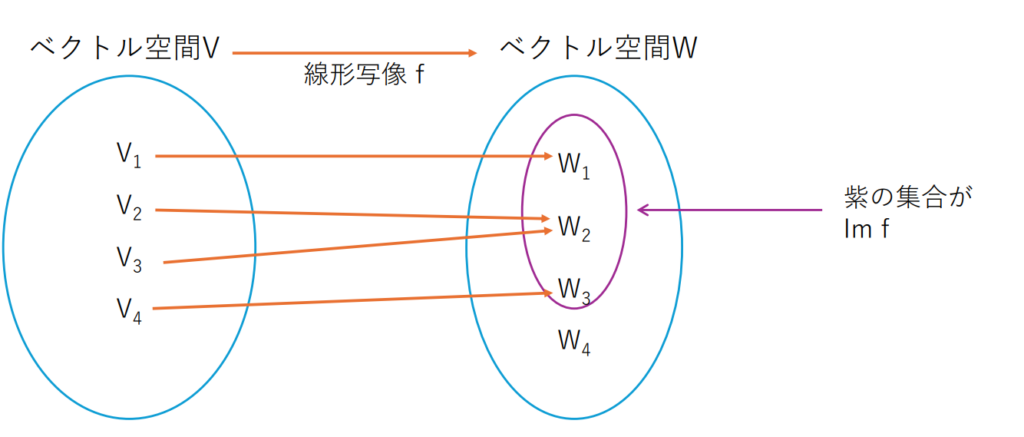
図のようにベクトル空間Vの要素を線形写像fによって、ベクトル空間Wに写しだした要素の集合が像なのです。
鏡や虫眼鏡の像を想像してみてください。鏡や虫眼鏡の像とは元の物体を写したものですよね。
核(カーネル)
定義
定義
線形写像 f がゼロベクトルに写すすべてのベクトルの集合
数式を用いて表すと次のようになります。(ここで、Ker (f)は f の核という意味です。)
\[
\text{Ker}(f) = \{ \mathbf{v} \in V \mid f(\mathbf{v}) = \mathbf{0} \}
\]
つまり、f(V)= 0 をみたす、すべての V が核となるわけです。これをゼロベクトルの逆像といいます。
核はとても大事な概念です。
方程式 \( A\mathbf{x} = \mathbf{b} \) の解を求める際、核は方程式 \( A\mathbf{x} = \mathbf{0} \) の解空間を表します。
つまり、\(\mathbf{x}_p\) を特解(方程式の特殊解)、\(\mathbf{v}\) を核の元とすると
$$
\mathbf{x} = \mathbf{x}_p + \mathbf{v} \quad (\mathbf{v} \in \text{Ker}(A))
$$
となり、線形写像の性質を理解するために必要不可欠なツールであるからです。
例題
では、早速例題を解いてみましょう。
例題1: 線形写像の核と像を求める
次の線形写像 \( f: \mathbb{R}^3 \to \mathbb{R}^2 \) を考えます。
$$
f \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x + 2y \\ 3y + z \end{pmatrix}
$$
1. この写像の核(カーネル) \(\text{Ker}(f)\) を求めよ。
例題解答
1. \(\text{Ker}(f)\) を求めるために、次の連立方程式を解きます。これは、核はゼロの逆像だからです。
$$
\begin{cases}
x + 2y = 0 \\
3y + z = 0
\end{cases}
$$
この連立方程式の解は、次のようになります。
$$
\begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} -2y \\ y \\ -3y \end{pmatrix} = y \begin{pmatrix} -2 \\ 1 \\ -3 \end{pmatrix}
$$
したがって、核は次のようになります。
$$
\text{Ker}(f) = \text{span} \left\{ \begin{pmatrix} -2 \\ 1 \\ -3 \end{pmatrix} \right\}
$$
ここで例えば$$\text{span s}$$とは、集合Sの一次結合 (線形結合)によってできるベクトル空間のことを指します。つまり、基底のことです。
練習問題
では、練習問題を解いてみましょう。
練習問題1:
次の線形写像 \( g: \mathbb{R}^4 \to \mathbb{R}^3 \) を考えます。
$$
g \begin{pmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{pmatrix} = \begin{pmatrix} x_1 – x_2 + x_3 \\ 2x_2 + x_4 \\ x_1 + x_3 + x_4 \end{pmatrix}
$$
1. この写像の核(カーネル) \(\text{Ker}(g)\) を求めよ。
解答
1. \(\text{Ker}(g)\) を求めるために、次の連立方程式を解きます。
$$
\begin{cases}
x_1 – x_2 + x_3 = 0 \\
2x_2 + x_4 = 0 \\
x_1 + x_3 + x_4 = 0
\end{cases}
$$
この連立方程式の解は、次のようになります。
$$
\begin{pmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{pmatrix} = t \begin{pmatrix} 1 \\ 0 \\ -1 \\ 0 \end{pmatrix}
$$
ここで、$$t=x_1$$です。
したがって、核は次のようになります。
$$
\text{Ker}(g) = \text{span} \left\{ \begin{pmatrix} 1 \\ 0 \\ -1 \\ 0 \end{pmatrix} \right\}
$$
練習問題2:
次の線形写像 \( k: \mathbb{R}^3 \to \mathbb{R}^3 \) を考えます。
$$
k \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x + y \\ y + z \\ z + x \end{pmatrix}
$$
1. この写像の核(カーネル) \(\text{Ker}(k)\) を求めよ。
解答
1. \(\text{Ker}(k)\) を求めるために、次の連立方程式を解きます。
$$
\begin{cases}
x + y = 0 \\
y + z = 0 \\
z + x = 0
\end{cases}
$$
この連立方程式の解は、次のようになります。
$$
x = y = z = 0
$$
したがって、核は次のようになります。
$$
\text{Ker}(k) = \left\{ \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} \right\}
$$
線形写像の像、核と次元の関係
線形写像の像、核には次の次元定理が成立します。
次元定理
\[
\text{dim}(\text{Im}(f)) + \text{dim}(\text{Ker}(f)) = \text{dim}(V)
\]
Im(f)は線形写像 f の像(イメージ)を指し、dimは次元を表します。
この定理は、線形写像の像の次元と核の次元の和が元のベクトル空間の次元に等しいことを示しています。
次元は後々説明しますが、次元とはベクトル空間を張る(構成する)ために必要なベクトルの数、つまり、基底の数です。
まとめ
今回学んだことは、次の4つでした。
・線形写像について
・像、核について
・核の求め方
・像、核の次元の関係
これらはすべて今後の線形代数の勉強の土台となる範囲なのでよく理解しておいてください。今回説明できなかった基底や次元については別の記事で扱います。


コメント